
The various geometric patterns found on a stopsign (photo by Aaron Zaremsky)
Patterns Within – A Geometric Study
- Published: April 4, 2016
This piece stems from a conversation I had a week or so ago with my older brother, who is a mathematics professor at Binghamton University. Most people, when faced with the notion of studying math, shrink away in horror. They want it out of the way and done with and left in high school notebooks. My brother relishes it, and specializes in a complex sub field of group theory that seems esoteric and incomprehensible to virgin eyes. Some would view his profession as undesirable and impractical, yet he is able to make a living doing research and teaching and does so at a university level, so take that.
I asked him if there were certain geometric patterns either in nature or in man made structures that would be able to be represented photographically. He rattled off a slew of geometric terms pertaining to objects and surfaces around us. Symmetries, groups, and reflections suddenly came pouring out of my consciousness from the world around me. I could see the patterns he spoke of and wanted to present them to my viewers with this essay.
I began with the man made, the objects in and around our town. Matthew described a number of symmetries found in the octagonal shape of a stop sign, rotational symmetry being the chief and most obvious. If you spin the stop sign any which way, it retains the same dimensions, hence, rotationally symmetric. A stop sign is also an example of reflective symmetry; the stop sign maintains its form when reflected. All of these rotations and reflections make up what is called a dihedral group, D8 in the case of a stop sign.
The many bricked alleyways, storefronts, and walkways in town are also laden with patterns. Most, if not all, brick layouts are a prime example of translational symmetry – an object slides, or glides along and retains its form, infinitely. Bricks do just that (until you get to the end of the wall, so infinity ends there.) They also inhabit the qualities of reflective symmetry, as discussed in the previous paragraph. In addition to these two symmetries, bricks are an example of a frieze group – a repetitive, two-dimensional pattern.
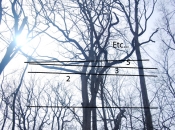
I then moved to the woods. Within the tangled wildness of nature there are structure and rules. Most plant growth patterns adhere to what is called The Fibonachi Sequence – 0, 1, 1, 2, 3, 5, 8, 13, 21, etc… (The previous number is added to the current to get the next, and so on). The sequence is related to what is called The Golden Ratio – a spiraling pattern with measurements dictated by the Fibonachi Sequence. You can find these patterns in the way tree limbs climb upwards and multiply and diverge from the trunk. They are also found in the spirals on the back of pine cones and numerous leaf arrangements. Scientists conjecture that these patterns are the most efficient means for plants to grow. It is a system for the plant to receive as many nutrients and sunlight as it can.
Why am I covering these patterns? Why do they matter and what could one benefit from studying them? I believe there are a few answers. Most of the math I do is in calculating tax returns, so it is useful to brush up and also study new stuff every now and then. Also, it is really interesting to study how these patterns form solid laws and patterns in our reality that hold up time and time again. I could also see many useful implications coming from a solid background in geometry. Any architectural design would benefit from knowing these laws, and perhaps agriculturalists could benefit from familiarizing themselves with the mathematical patterns found in nature. The world is for us to explore and study.
2 Responses to “Patterns Within – A Geometric Study”
The Yellow Springs News encourages respectful discussion of this article.
You must login to post a comment.
Don't have a login? Register for a free YSNews.com account.
























Hello!
You would have to talk to my brother, he’s the expert not me.
You can reach him at zaremsky@math.binghamton.edu.
We both attended third grade in Yellow Springs so why not help those in the same situation we were in twenty or so years ago 🙂
Hello, This is Ms. Morgan’s Third Grade T.E.A.M. We want to comment about this geometric article because we are working on a project about geometry in Yellow Springs. We used the photographs in this article to identify many different quadrilaterals. The story made us think about our work. Thank you for the helpful pictures and text. We hope to report on our work. Maybe you can help us with this. It is exciting to discover math in our world. Sincerely, Ms. Morgan’s Third Grade T.E.A.M.